Walkthrough

Diberikan sebuah binary .ko (kernel module) bernama ghost.ko. Karena ini adalah kernel module, kita bisa expect ada init function dan exit function.

Langsung aja buka di IDA/Ghidra.

1. Analysis: The Init Function

Di fungsi ghost_init, kita melihat ada beberapa setup penting.

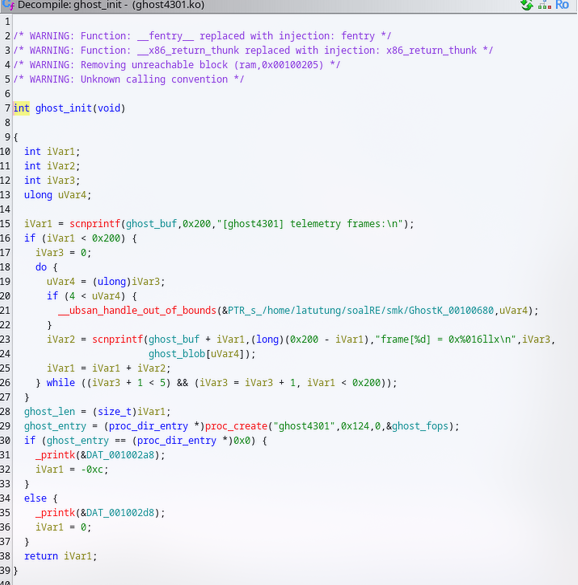
Module ini mencoba membuat entry di /proc/ghost4301. Hal yang menarik ada di logic pengecekannya:

1
    ghost_len = i;
2
    uint64_t rax_1 = proc_create("ghost4301", 0x124, 0, &ghost_fops);
3
    ghost_entry = rax_1;
4

5
    if (!rax_1)
6
        _printk(0x400210, "ghost4301");
7
    else
8
    {
9
        _printk(0x4002b1,
10
            "ghost4301_telemetry\nz[i] = rotl8((flag[i]^key[i%7] + poly(i)), (3*i)%8)\npoly(i) = i^3 + "
11
        "7*i^2 + 13*i + 37 (mod 256)\n");
12
        _printk(0x4002b1, "key[7] = {0x13,0x37,0x42,0xA5,0x5C,0x9E,0x11}\n");
13
        _printk(0x400238, "ghost4301");
14
    }

Jika proc_create BERHASIL (rax_1 != 0), dia malah nge-print “telemetry” yang berisi rumus enkripsi dan key-nya. Ini behaviour yang agak unik, biasanya error message yang diprint kalau gagal.

Dari printk tersebut, kita dapat informasi vital:

Encryption Formula: z[i] = rotl8((flag[i]^key[i%7] + poly(i)), (3*i)%8)
Key: {0x13, 0x37, 0x42, 0xA5, 0x5C, 0x9E, 0x11}
Polynomial: poly(i) = i^3 + 7*i^2 + 13*i + 37 (mod 256)

2. Extracting the Ciphertext

Kalau kita lihat di awal fungsi ghost_init, ada loop yang nge-print “telemetry frames”:

1
            i += scnprintf(i + &ghost_buf, 0x200 - i, "frame[%d] = 0x%016llx\n", rcx_1,
2
                *((r14_1 << 3) + &ghost_blob));

Loop ini membaca data dari ghost_blob dan menampilkannya sebagai 64-bit integers (0x%016llx).

Kita bisa ekstrak data ini langsung dari file binary .ko menggunakan readelf atau objdump. Kita cari section .rodata atau symbol ghost_blob.

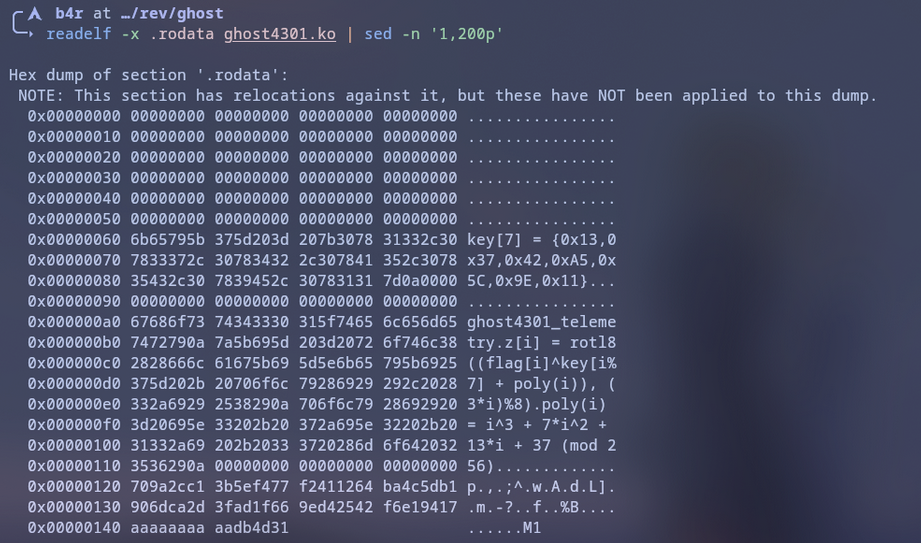
Kita temukan blok data 40 bytes yang mencurigakan di string dump atau rodata:

1
70 9A 2C C1 3B 5E F4 77
2
F2 41 12 64 BA 4C 5D B1
3
90 6D CA 2D 3F AD 1F 66
4
9E D4 25 42 F6 E1 94 17
5
AA AA AA AA AA DB 4D 31

Ini kemungkinan besar adalah ciphertext z kita.

3. The Solver Strategy

Dari rumus enkripsi: z[i] = rotl8((flag[i] ^ key[i%7] + poly(i)), (3*i)%8)

Kita harus melakukan operasi kebalikannya (decryption) urut dari luar ke dalam:

Rotate Right: Kebalikan dari rotl8 adalah rotr8.
Subtract Poly: Kebalikan dari + poly(i) adalah - poly(i).
XOR Key: Kebalikan dari ^ key adalah ^ key (XOR adalah inversenya sendiri).

Jadi rumus dekripsinya: flag[i] = rotr8(z[i], (3*i)%8) - poly(i) ^ key[i%7]

Attempt 1: Naive Solve

Awalnya gw coba solve langsung byte-per-byte sesuai urutan dump:

1
z_raw = bytes.fromhex("""
2
70 9A 2C C1 3B 5E F4 77
3
F2 41 12 64 BA 4C 5D B1
4
90 6D CA 2D 3F AD 1F 66
5
9E D4 25 42 F6 E1 94 17
6
AA AA AA AA AA DB 4D 31
7
""")
8
# ... decryption loop ...

Tapi hasilnya gagal. Outputnya cuma sampah binary yang gak membentuk flag.`

Attempt 2: Addressing Endianness

Gw sadar ada yang aneh. Di code ghost_init, data dibaca sebagai unsigned long long (64-bit) dan diprint dengan format %016llx.

1
*((r14_1 << 3) + &ghost_blob)

Di arsitektur x86 (Little Endian), ketika kita baca 8 byte “A B C D E F G H” sebagai satu integer 64-bit, nilainya jadi 0xHGFEDCBA.

Jadi, data raw yang kita copy (kalau kita asumsi itu dari print output atau cara storage kernel) perlu kita reverse per 8 byte untuk mendapatkan urutan byte asli yang dimaksud oleh enkripsi byte-per-byte.

Code fix-nya:

1
z = b''.join(
2
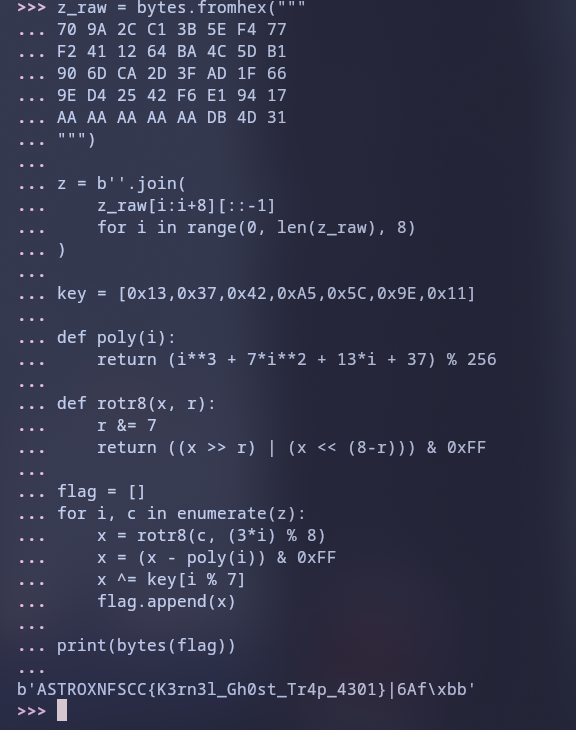
    z_raw[i:i+8][::-1]
3
    for i in range(0, len(z_raw), 8)
4
)

4. Final Solver Script

Berikut script solver lengkapnya:

1
z_raw = bytes.fromhex("""
2
70 9A 2C C1 3B 5E F4 77
3
F2 41 12 64 BA 4C 5D B1
4
90 6D CA 2D 3F AD 1F 66
5
9E D4 25 42 F6 E1 94 17
6
AA AA AA AA AA DB 4D 31
7
""")
8

9
# Reverse every 8 bytes chunk to fix endianness
10
z = b''.join(
11
    z_raw[i:i+8][::-1]
12
    for i in range(0, len(z_raw), 8)
13
)
14

15
key = [0x13,0x37,0x42,0xA5,0x5C,0x9E,0x11]
16

17
def poly(i):
18
    return (i**3 + 7*i**2 + 13*i + 37) % 256
19

20
def rotr8(x, r):
21
    r &= 7
22
    return ((x >> r) | (x << (8-r))) & 0xFF
23

24
flag = []
25
for i, c in enumerate(z):
26
    # 1. Reverse rotation
27
    x = rotr8(c, (3*i) % 8)
28

29
    # 2. Reverse addition (subtract)
30
    x = (x - poly(i)) & 0xFF
31

32
    # 3. Reverse XOR
33
    x ^= key[i % 7]
34

35
    flag.append(x)
36

37
print(bytes(flag))

reversing linux kernel is easy (?)